آیا به شغلی در امنیت سایبری امیدوار هستید؟ این مهم است که شما هم کمی از ریاضیات درک داشته باشید. در اینجا دلیل آن است.
برای اینکه بیشتر فناوری ها قابل استفاده باشند، کارهای بسیار پیچیده در پس زمینه انجام می شود. اکثر مردم از یک سیستم عامل استفاده می کنند و اهمیتی نمی دهند که چرا و چگونه وجود دارد. لازم به نظر نمی رسد. در سالهای اولیه محاسبات، کدهای ماشین و ریاضیات بسیار مهمتر بودند. اما اگر حرفه ای در زمینه امنیت سایبری هستید، ریاضیات همچنان برای شما مهم است. چرا؟ به هر حال ریاضی چه نقشی در امنیت سایبری دارد؟
چگونه از فرمول های ریاضی در امنیت سایبری استفاده می شود؟
فرمولها، الگوریتمها و نظریهها با دنیای مهندسی برق و الکترونیک ترکیب شدند و به رایانهها منجر شدند. اگر یک متخصص امنیت سایبری بخواهد در مورد کامپیوتر بیاموزد و هدفش یک حرفه خوب در این زمینه باشد، باید برخی از پیش فرض ها را در مورد ریاضیات بشکند.
چگونه از فیلتر استفاده می شود؟
روش های فیلتر به طور فعال برای بسیاری از مشکلات مختلف استفاده می شود. اگر از منظر امنیت سایبری به موضوع نگاه کنیم، بهتر است فهرست سیاه را به عنوان مثال در نظر بگیریم.
فرض کنید می خواهید از منطق لیست سیاه برای مسدود کردن IP در فایروال استفاده کنید. برای این کار، سیستمی که می خواهید ایجاد کنید باید درخواست ورودی را به مکانیزم کنترل ارسال کند و آدرس IP بسته را در لیست جستجو کند. اگر آدرس IP بسته در این لیست وجود داشته باشد، اجازه عبور را نمی دهد. نمایش ریاضی این عملیات به شرح زیر است:
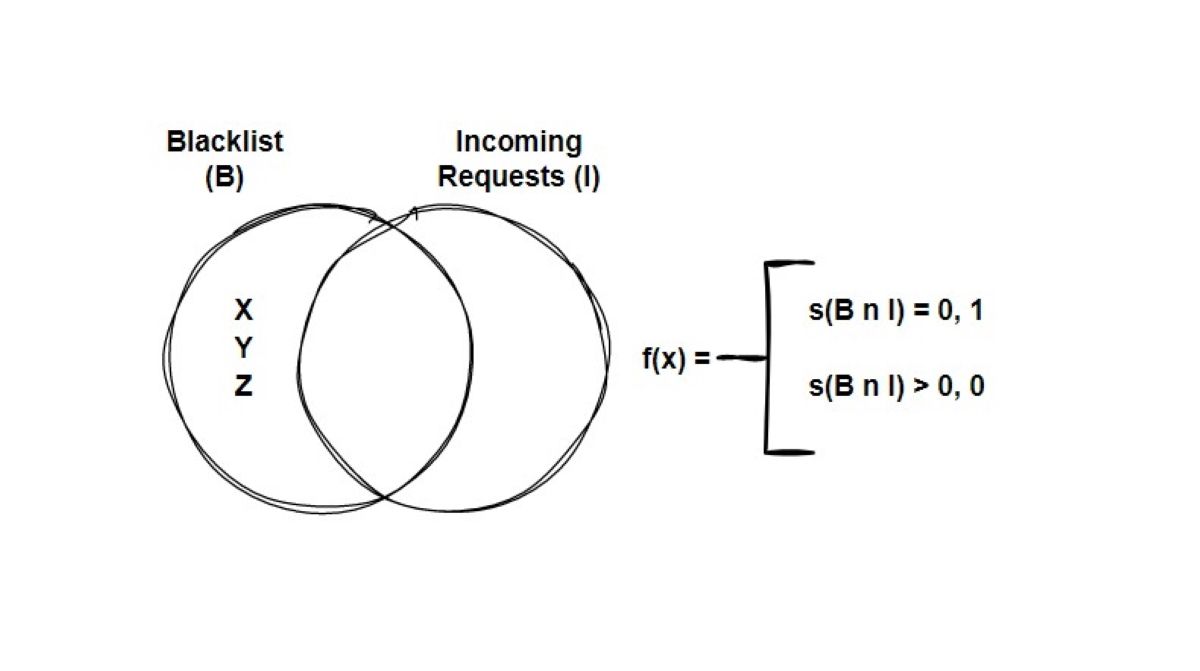
همانطور که از نمودار می بینید، اگر نتیجه مطابق تابع f(x) 1 باشد، انتقال مجاز است. در غیر این صورت، اینطور نیست. به این ترتیب، درخواستها را فیلتر میکنید و فقط از طریق IPهایی که میخواهید اجازه میدهید.
روش مقیاس بندی چیست؟
برای اطمینان از امنیت یک سیستم، ابتدا باید مقیاس پذیر باشد. برای بررسی روش مقیاس بندی از منظر امنیتی، اجازه دهید یک وب سرور را در نظر بگیریم. هدف این است که از نظر تئوری حجم کار روی وب سرور محاسبه شود.
برای درک حجم کار در وب سرور، باید یک سوال مهم را در نظر بگیرید: اگر میانگین زمان سپری شده بین درخواست های دریافتی 100 میلی ثانیه (میلی ثانیه) باشد، به طور متوسط در یک ثانیه چند درخواست دریافت می شود؟
برای توصیف ریاضی این موضوع، اجازه دهید برای مقدار مجهول یک نام بگذاریم. به عنوان مثال، اجازه دهید T یک متغیر تصادفی باشد که زمان سپری شده بین درخواست ها به سرور را نشان می دهد.
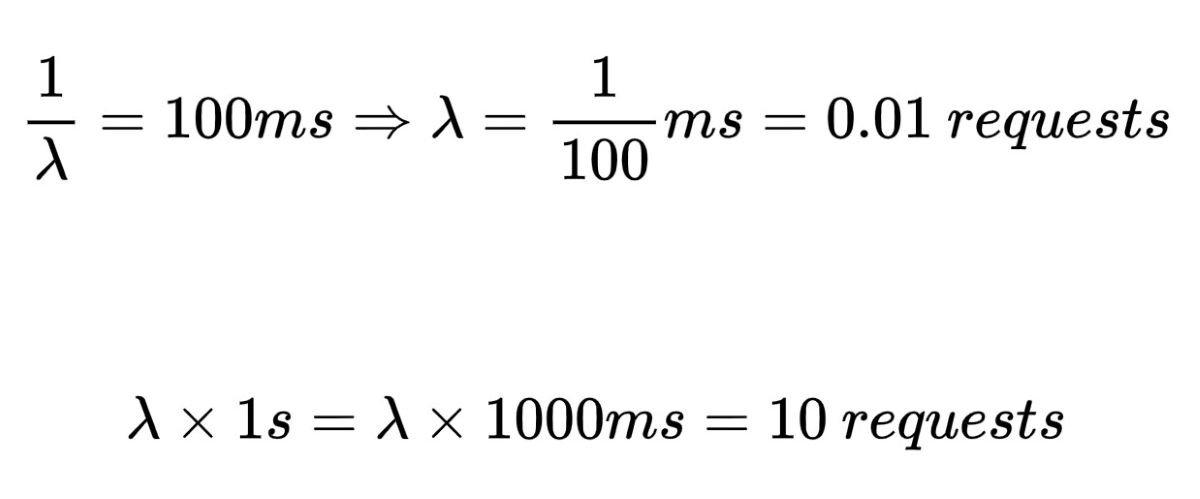
در نتیجه، با تغییر مقیاس 100 میلیثانیه به 1 میلیثانیه، 0.01 درخواست در واحد زمان دریافت میکنید. این بدان معناست که شما می توانید به طور متوسط 10 درخواست در 1000 میلی ثانیه دریافت کنید.
اهرم احتمال خطا
ممکن است لازم باشد بدانید چند درصد از نتایج تولید شده توسط یک محصول مدیریت اطلاعات امنیتی و رویداد (SIEM) “مثبت کاذب” است. محصولات SIEM یکی از ساده ترین نمونه های استفاده از احتمالات خطا هستند. البته حتی در تست های نفوذ نیز می توانید از احتمالات خطا استفاده کنید و بر اساس نتایج موجود بردار حمله را در نظر بگیرید. بیایید از یک مثال استفاده کنیم.
احتمال خطا در انتقال اعداد باینری روی یک شبکه کامپیوتری که با یک میلیارد بیت در ثانیه کار می کند تقریباً 10 توان منهای 8 است. احتمال پنج یا بیشتر خطا در یک ثانیه چقدر است؟
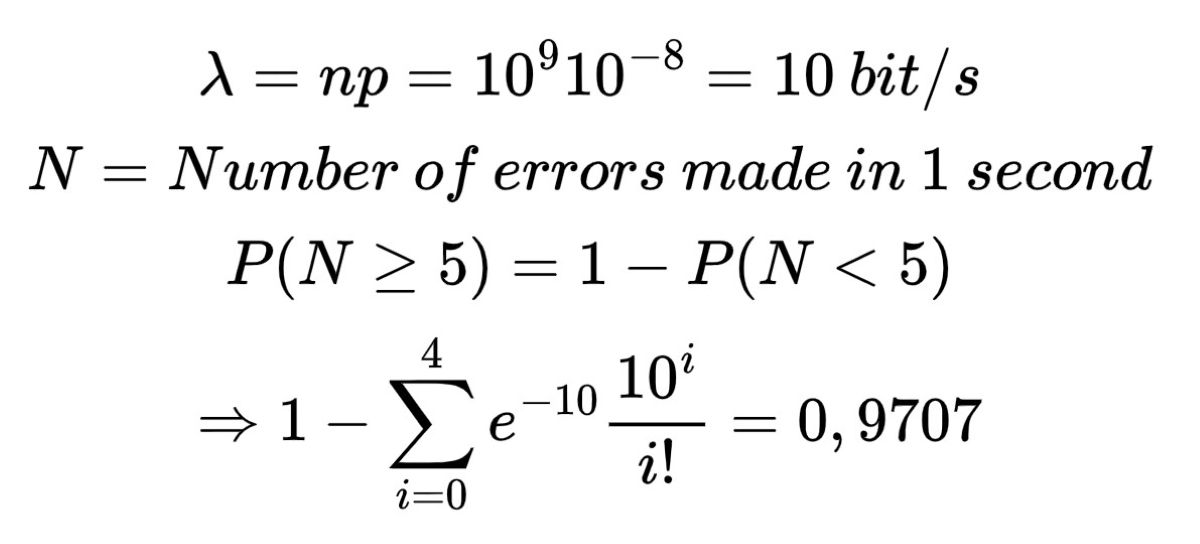
یافتن این احتمالات خطا و به حداقل رساندن آنها به شما ایده ای برای دستیابی به یک سیستم قوی تر و ایمن تر می دهد.
چگونه مهندسی اجتماعی از مدل مارکوف استفاده می کند
مدل مارکوف یک مدل سازی آماری از انتقال بین گره ها است. به عبارت دیگر، اگر حالت مارکوف را برای توییت های یک کاربر توییتر اعمال کنید، می توانید یک توییت جدید از کلماتی که قبلاً توسط آن کاربر استفاده شده است ایجاد کنید. این الگویی است که بسیاری از ابزارهای تولید توییت نیز از آن استفاده می کنند. از منظر امنیت سایبری، مهاجمان می توانند از این روش برای حملات مهندسی اجتماعی استفاده کنند.
به عنوان مثال، اگر یک مهاجم بتواند پیام های شخص را ضبط کند، می تواند از پیام ها برای ایجاد یک مدل مارکوف استفاده کند. مهاجم می تواند پیامی را با توجه به نتیجه به دست آمده از مدل بنویسد و شخصی که آن را می خواند ممکن است فکر کند که این پیام واقعی است. این در مورد هر پیامی مانند ایمیل ها و رسانه های اجتماعی صدق می کند، اما همچنین در مورد اسناد خطرناک تر مانند صورتحساب های بانکی، مکاتبات رسمی و اسناد دولتی نیز صدق می کند. به همین دلیل است که باید پرچمهای قرمز فیشینگ را بدانید که باید مراقب آنها باشید.
اگر می خواهید ببینید که مدل مارکوف چگونه از طریق یک الگوریتم کار می کند، می توانید کدهای موجود در GitHub را بررسی کنید.
مثال تئوری بازی ها
تئوری بازی را به عنوان تضاد بین موقعیت برد بازیکن در یک بازی و موقعیت باخت سایر بازیکنان در نظر بگیرید. به طور خلاصه، برای بردن یک بازی، حریفان شما باید ببازند. به همین ترتیب، برای اینکه حریفان ببازند، شما باید برنده شوید.
توانایی بررسی نظریه بازی ها از منظر امنیت سایبری می تواند به شما در گرفتن بهترین تصمیم در هر شرایط بحرانی کمک کند. به عنوان مثال، تصور کنید دو بانک رسمی وجود دارد، ABC و XYZ.
بانک ABC از یک اقدام امنیتی خاص برای مبارزه با تهدیدات باج افزار استفاده می کند. بانک ABC می خواهد این اقدام امنیتی را در ازای کارمزد به بانک XYZ بفروشد. آیا واقعاً لازم است بانک XYZ اطلاعاتی در مورد این اقدام امنیتی دریافت کند؟
- هزینه اطلاعات = X
- هزینه عدم وجود اطلاعات = Y
- ارزش اطلاعات = Z
- اگر بانک اطلاعات را بخرد = Z – X سود
در صورتی که بانک XYZ اطلاعات را خریداری کند و اقدامی انجام ندهد، متحمل ضرری معادل (X+Y) خواهد شد. و بنابراین، بانک XYZ می تواند پس از در نظر گرفتن همه احتمالات، از داده های عددی خود برای اتخاذ مناسب ترین تصمیم استفاده کند. شما می توانید از بسیاری از روش های تئوری بازی بهره مند شوید، به ویژه برای متقاعد کردن واحدهای محافظت شده توسط یک دفتر امنیت سایبری که آگاهی ریاضی را توسعه نداده است و برای ارائه اطلاعات سایبری در مورد این مسائل.
فاز مدلسازی
مدل سازی و تحلیل قابل مشاهده همیشه نتیجه می دهد. بخش بزرگی از امنیت سایبری شامل مراحل جمع آوری اطلاعات و اطلاعات است. به همین دلیل مدلینگ هم برای حمله و هم برای دفاع از اهمیت ویژه ای برخوردار است. اینجاست که نظریه گراف وارد می شود – روشی که اغلب توسط پلتفرم های شبکه های اجتماعی مانند فیس بوک و توییتر استفاده می شود.
اکثر شبکه های اجتماعی معروف صفحات خود را مانند نکات برجسته، داستان ها و پست های محبوب با استفاده از نظریه گراف سازماندهی می کنند. در اینجا یک مثال ساده از روش نمودار مورد استفاده در رسانه های اجتماعی آورده شده است:
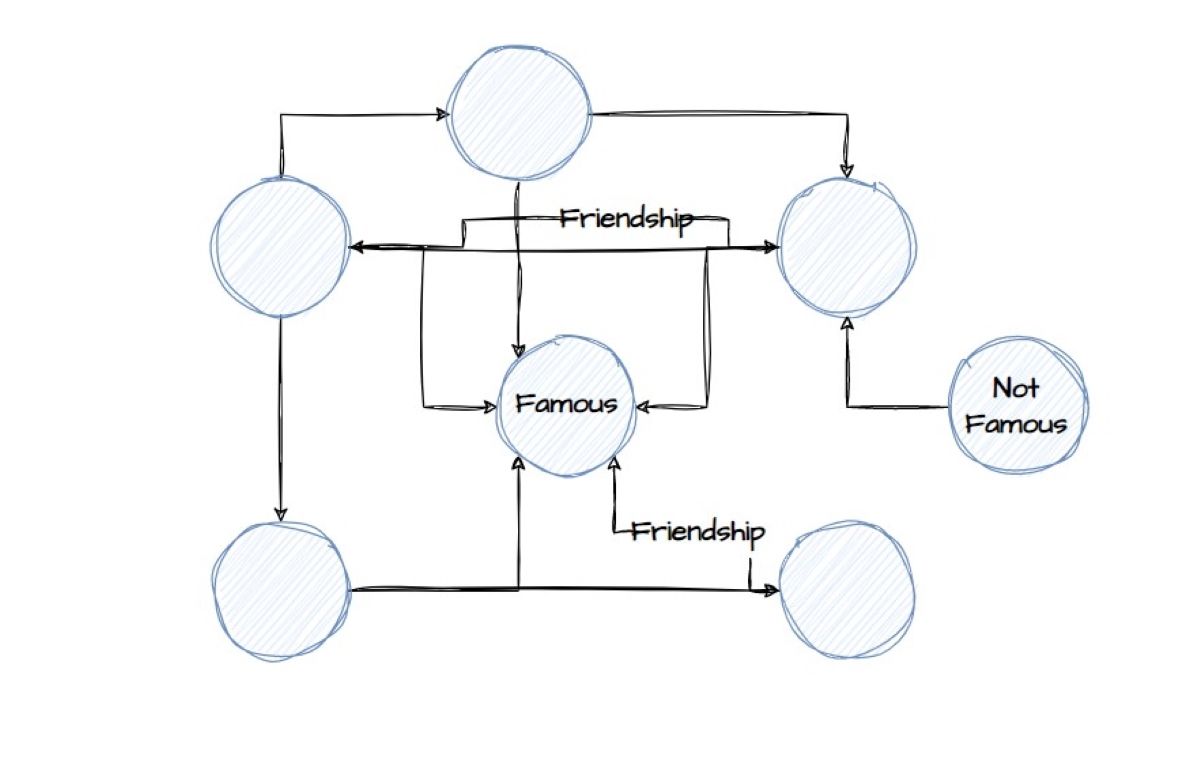
به طور خلاصه، نظریه گراف برای یک متخصص امنیت سایبری بسیار مفید است تا بتواند ترافیک شبکه را تجزیه و تحلیل کند و جریان شبکه را مدل کند.
ریاضیات در روش های رمزنگاری و رمزگذاری
اگر میدانید توابع چگونه کار میکنند، میتوانید به راحتی درباره رمزنگاری و هش کردن نیز بیاموزید. به عبارت ساده، عملکردها مانند یک مرکز تولید هستند. شما چیزی را داخل تابع می اندازید و نتیجه ای برای شما ایجاد می کند. شما می توانید تابع را تغییر دهید، یعنی قوانینی را تنظیم کنید و نتیجه را همانطور که می خواهید بگیرید.
این توابع در بین خود به دسته های مختلفی تقسیم می شوند. با این حال، از آنجایی که داشتن یک رمز عبور قوی و نشکن حیاتی است، ما فقط عملکردهای یک طرفه را پوشش خواهیم داد. اگر طبق مثال امکانات تولید به عملکردهای یک طرفه فکر کنید، آنها توابعی هستند که نمی توانند نتیجه تولید شده را بازیابی کنند. بنابراین شما یک خروجی دریافت خواهید کرد، اما این خروجی همانطور که هست باقی می ماند. مهندسی معکوس وجود ندارد
بهترین منطقه برای استفاده از این قطعا در رمزگذاری است. برای مثال، توابع هش اینگونه کار می کنند. اگر متنی را از طریق تابع هش عبور دهید، مقدار کاملا متفاوتی به شما می دهد. این مقدار دیگر قابل برگشت نیست، بنابراین می توانید متن خود را مخفی و ایمن کنید.
آیا واقعاً به دانستن ریاضیات نیاز دارم؟
اگر با آسیب پذیری در صدها فایل و ده ها هزار خط کد سر و کار دارید. وب سایتی که صدها هزار بازدید کننده دارد. یا یک برنامه بانکی که در آن مردم صورتحساب های خود را پرداخت می کنند … ممکن است مجبور شوید از ریاضیات استفاده کنید. در غیر این صورت از کار خود بیکار نخواهید شد. اما درک عمیق ریاضی شما را یک قدم جلوتر میگذارد.
