بیش از یک راه برای بازدید از تمام گره ها در یک BST وجود دارد.
درختان باینری یکی از پرکاربردترین ساختارهای داده در برنامه نویسی هستند. درخت جستجوی دودویی (BST) اجازه می دهد تا داده ها را در قالب گره ها (گره والد و گره فرزند) ذخیره کند به طوری که گره فرزند سمت چپ کوچکتر از گره والد و گره فرزند سمت راست بزرگتر باشد.
درختهای جستجوی دودویی عملیات پیمایش، جستجو، حذف و درج کارآمد را ممکن میسازند. در این مقاله، با سه روش پیمایش درخت جستجوی دودویی آشنا خواهید شد: پیمایش پیش سفارش، پیمایش نامرتب و پیمایش پس سفارش.
پیمایش Inorder
پیمایش inorder فرآیند پیمایش گرههای یک درخت جستجوی دودویی با پردازش بازگشتی زیردرخت سمت چپ، سپس پردازش گره ریشه و در نهایت پردازش بازگشتی زیردرخت سمت راست است. از آنجایی که گره ها را به ترتیب ارزش صعودی پردازش می کند، این تکنیک را پیمایش نامرتب می نامند.
پیمایش فرآیند بازدید از هر گره در ساختار داده درختی دقیقاً یک بار است.
الگوریتم پیمایش نامتناسب
برای عبور از تمام گره های BST این کار را تکرار کنید:
- به صورت بازگشتی زیر درخت سمت چپ را طی کنید.
- از گره ریشه بازدید کنید.
- به صورت بازگشتی زیر درخت سمت راست را طی کنید.
تجسم پیمایش بی نظم
یک مثال بصری می تواند به توضیح پیمایش درخت جستجوی دودویی کمک کند. این شکل پیمایش نامرتب یک درخت جستجوی باینری مثال را نشان می دهد:
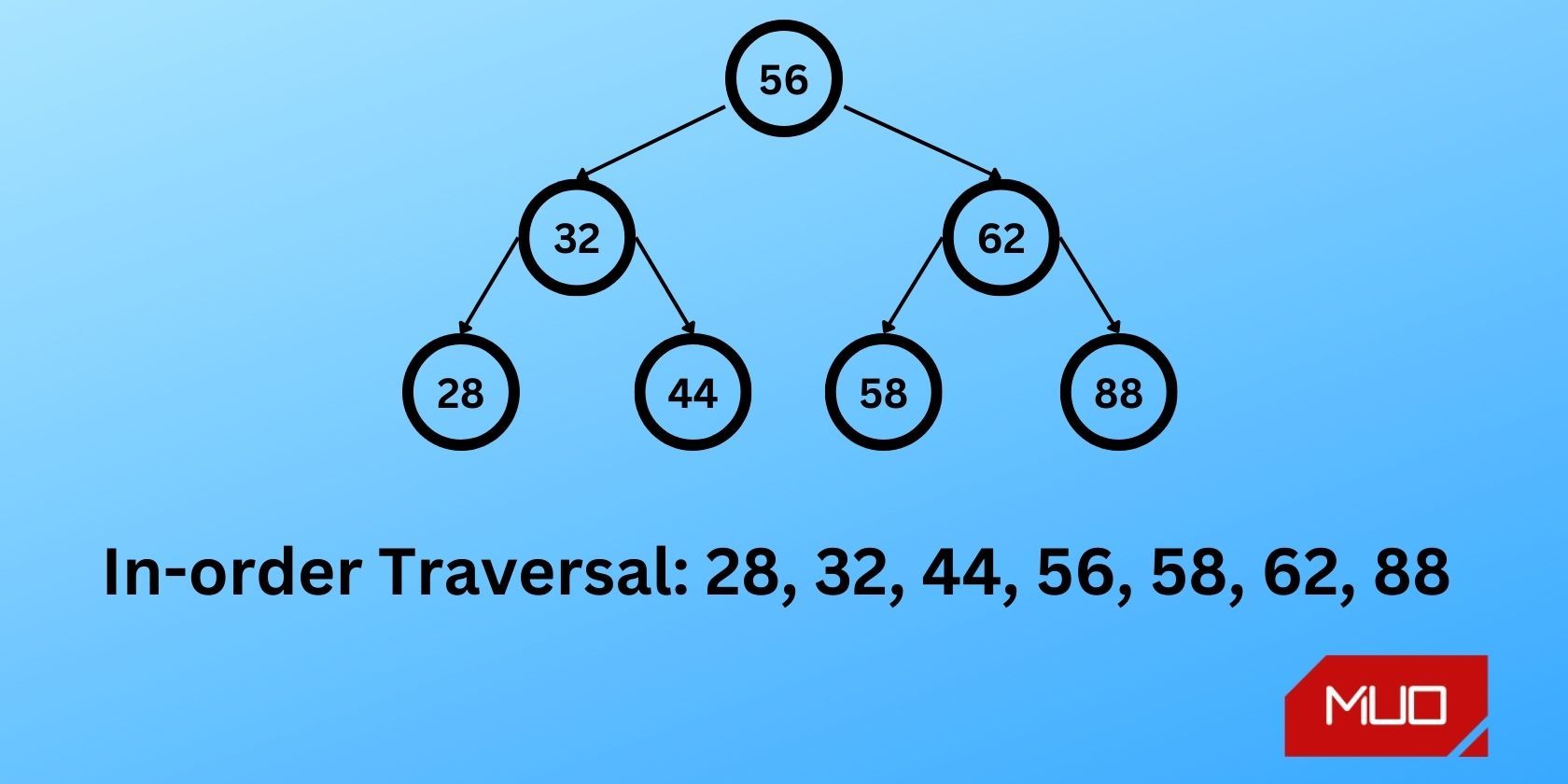
در این درخت جستجوی دودویی، 56 گره ریشه است. ابتدا باید زیر درخت 32 سمت چپ و سپس گره ریشه 56 و سپس زیر درخت سمت راست 62 را طی کنید.
برای زیردرخت 32، ابتدا زیر درخت سمت چپ، 28 را طی کنید. در مرحله بعد، زیر درخت سمت راست، 44 را که فرزندی نیز ندارد، طی کنید. بنابراین ترتیب پیمایش برای زیردرختی که در 32 ریشه دارد، 28 -> 32 -> 44 است.
بعد، از گره ریشه، 56 دیدن کنید.
سپس، زیر درخت سمت راست را که در 62 ریشه دارد، پیمایش کنید. با پیمایش زیردرخت سمت چپ آن، با ریشه 58 شروع کنید. هیچ فرزندی ندارد، پس از گره 62 بازدید کنید. در نهایت، زیر درخت سمت راست، 88، که آن نیز فرزندی ندارد، عبور دهید.
بنابراین الگوریتم گره های درخت را به ترتیب زیر بازدید می کند:
28 -> 32 -> 44 -> 56 -> 58 -> 62 -> 88
کاربرد Inorder Traversal
برای بدست آوردن مقادیر عناصر گره به ترتیب فزاینده می توانید از پیمایش inorder استفاده کنید. برای بدست آوردن مقادیر به ترتیب کاهشی، به سادگی فرآیند را معکوس کنید: از زیردرخت سمت راست، سپس گره ریشه و سپس زیر درخت سمت چپ بازدید کنید. می توانید از الگوریتم برای یافتن پیشوند یک درخت بیان استفاده کنید.
پیمایش پیشسفارش کنید
پیمایش پیش سفارش مشابه inorder است، اما قبل از پردازش بازگشتی زیردرخت سمت چپ و سپس زیردرخت سمت راست، گره ریشه را پردازش می کند.
الگوریتم پیمایش پیش سفارش
برای عبور از تمام گره های BST این کار را تکرار کنید:
- از گره ریشه بازدید کنید.
- به صورت بازگشتی زیر درخت سمت چپ را طی کنید.
- به صورت بازگشتی زیر درخت سمت راست را طی کنید.
تجسم پیمایش پیشسفارش
شکل زیر پیمایش پیش سفارش درخت جستجوی باینری را نشان می دهد:
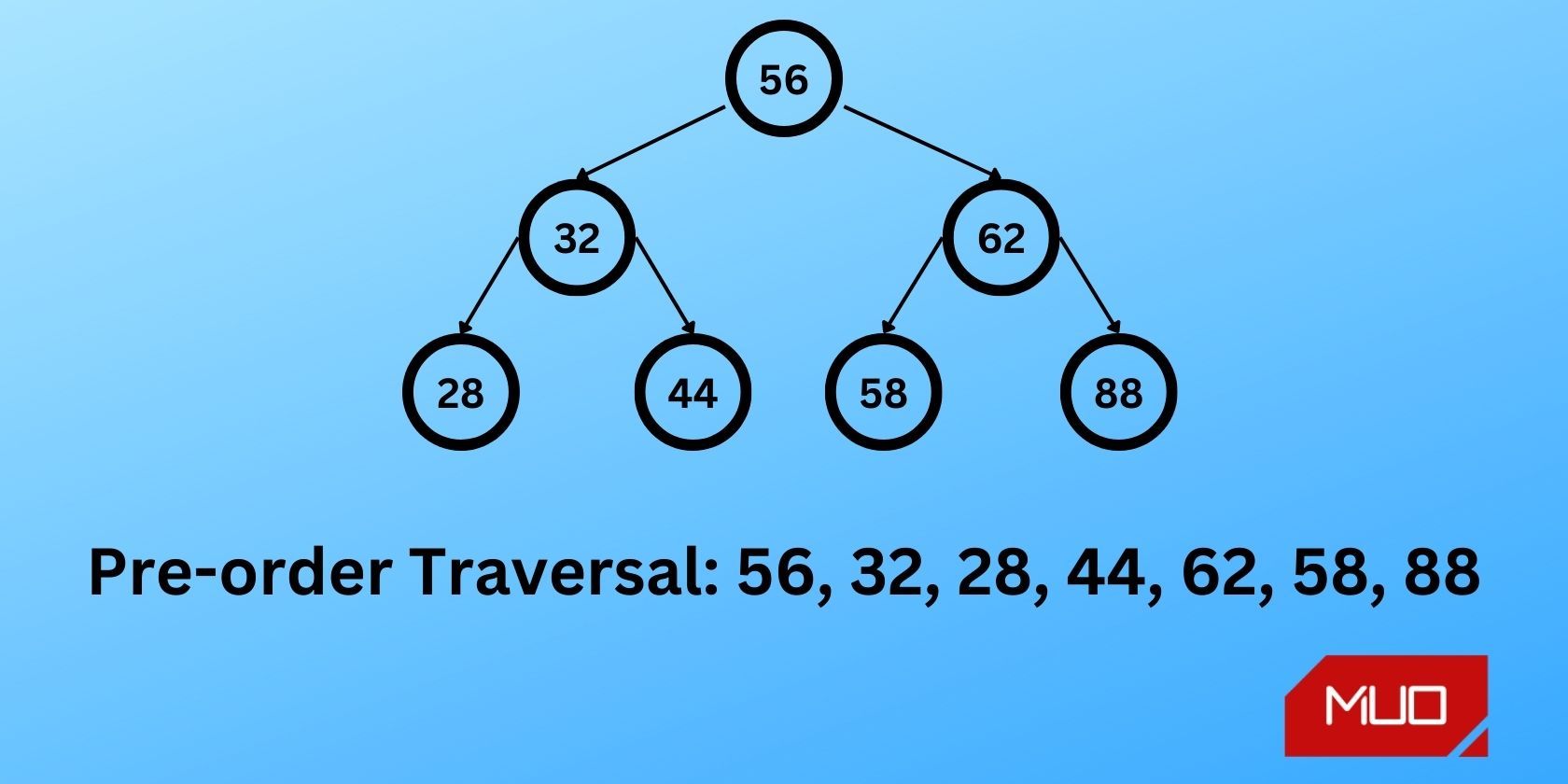
در این درخت جستجوی دودویی، با پردازش گره ریشه، 56، شروع کنید. سپس زیر درخت سمت چپ، 32، و سپس زیر درخت سمت راست، 62 را طی کنید.
برای زیردرخت سمت چپ، مقدار را در گره ریشه، 32 پردازش کنید. سپس، زیر درخت سمت چپ، 28، و در نهایت زیر درخت سمت راست، 44 را طی کنید. این پیمایش زیردرخت سمت چپ را که ریشه در 32 دارد، کامل میکند. پیمایش به ترتیب زیر انجام میشود. : 56 -> 32 -> 28 -> 44.
برای زیردرخت سمت راست، مقدار را در گره ریشه، 62 پردازش کنید. سپس، زیر درخت سمت چپ، 58، و در نهایت زیر درخت سمت راست، 88 را طی کنید. باز هم، هیچ یک از گره ها فرزندی ندارند، بنابراین پیمایش در این مرحله کامل می شود.
شما درخت کامل را به ترتیب زیر طی کرده اید:
56 -> 32 -> 28 -> 44 -> 62 -> 58 -> 88
کاربرد پیمایش پیش سفارش
شما می توانید از پیمایش پیش سفارش برای ایجاد یک کپی از درخت به راحتی استفاده کنید.
پیمایش پست سفارش
پیمایش postorder فرآیند پیمایش گرههای یک درخت جستجوی دودویی با پردازش بازگشتی زیردرخت سمت چپ، سپس پردازش بازگشتی زیردرخت سمت راست و در نهایت پردازش گره ریشه است. از آنجایی که گره ریشه را بعد از هر دو زیردرخت پردازش می کند، به این روش پیمایش postorder گفته می شود.
الگوریتم پیمایش پس سفارش
برای عبور از تمام گره های BST این کار را تکرار کنید:
- به صورت بازگشتی زیر درخت سمت چپ را طی کنید.
- به صورت بازگشتی زیر درخت سمت راست را طی کنید.
- از گره ریشه بازدید کنید.
تجسم پیمایش سفارش پست
شکل زیر پیمایش postorder درخت جستجوی باینری را نشان می دهد:
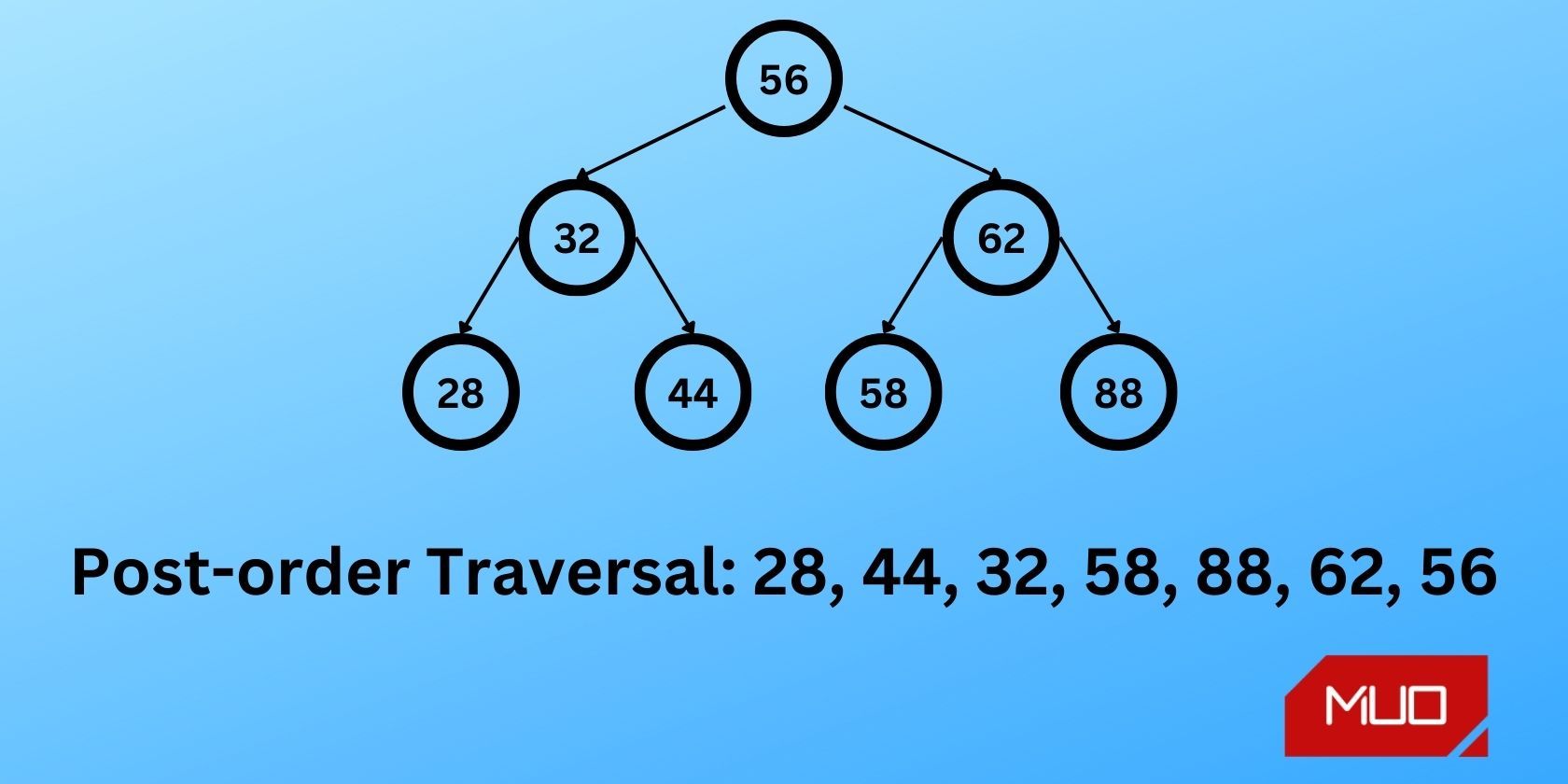
با پیمایش زیر درخت سمت چپ، 32، سپس زیر درخت سمت راست، 62 شروع کنید. با پردازش گره ریشه، 56 به پایان برسانید.
برای پردازش درخت فرعی که در 32 ریشه دارد، زیر درخت سمت چپ آن، 28 را طی کنید. از آنجایی که 28 فرزندی ندارد، به زیردرخت سمت راست بروید، 44. پردازش 44 را انجام دهید، زیرا آن نیز فرزندی ندارد. در نهایت، گره ریشه، 32 را پردازش کنید. شما این زیردرخت را به ترتیب 28 -> 44 -> 32 طی کرده اید.
زیردرخت سمت راست را با استفاده از همان رویکرد برای بازدید از گره ها به ترتیب 58 -> 88 → 62 پردازش کنید.
در نهایت، گره ریشه، 56 را پردازش کنید. درخت کامل را به ترتیب زیر طی خواهید کرد:
28 -> 44 -> 32 -> 58 -> 88 -> 62 -> 56
کاربرد پیمایش Postorder
می توانید از پیمایش postorder برای حذف یک درخت از برگ تا ریشه استفاده کنید. همچنین می توانید از آن برای یافتن عبارت postfix درخت عبارت استفاده کنید.
برای بازدید از تمام گره های برگ یک گره خاص قبل از بازدید از خود گره، می توانید از تکنیک پیمایش postorder استفاده کنید.
پیچیدگی زمانی و مکانی پیمایش درخت جستجوی دودویی
پیچیدگی زمانی هر سه تکنیک پیمایش O(n) است که n اندازه درخت دودویی است. پیچیدگی فضایی همه تکنیکهای پیمایش O(h) است که h ارتفاع درخت دودویی است.
اندازه درخت دودویی برابر است با تعداد گره های آن درخت. ارتفاع درخت دودویی تعداد لبه های بین گره ریشه درخت و دورترین گره برگ آن است.
کد پایتون برای پیمایش درخت جستجوی باینری
در زیر یک برنامه پایتون برای انجام هر سه پیمایش درخت جستجوی باینری وجود دارد:
# Node class is used to create individual nodes
# of the Binary Search Tree (BST)
class Node:
def __init__(self, element):
self.left = None
self.right = None
self.value = element
# Function to perform the inorder tree traversal
def inorder(root):
if root:
# Traverse left subtree
inorder(root.left)
# Traverse root
print(str(root.value) + ", ", end='')
# Traverse right subtree
inorder(root.right)
# Function to perform the postorder tree traversal
def postorder(root):
if root:
# Traverse left subtree
postorder(root.left)
# Traverse right subtree
postorder(root.right)
# Traverse root
print(str(root.value) + ", ", end='')
# Function to perform the preorder tree traversal
def preorder(root):
if root:
# Traverse root
print(str(root.value) + ", ", end='')
# Traverse left subtree
preorder(root.left)
# Traverse right subtree
preorder(root.right)
# Creating nodes of the tree
root = Node(56)
root.left = Node(32)
root.right = Node(62)
root.left.left = Node(28)
root.left.right = Node(44)
root.right.left = Node(58)
root.right.right = Node(88)
print("Inorder Traversal of BST: ")
inorder(root)
print()
print("Preorder Traversal of BST: ")
preorder(root)
print()
print("Postorder Traversal of BST: ")
postorder(root)
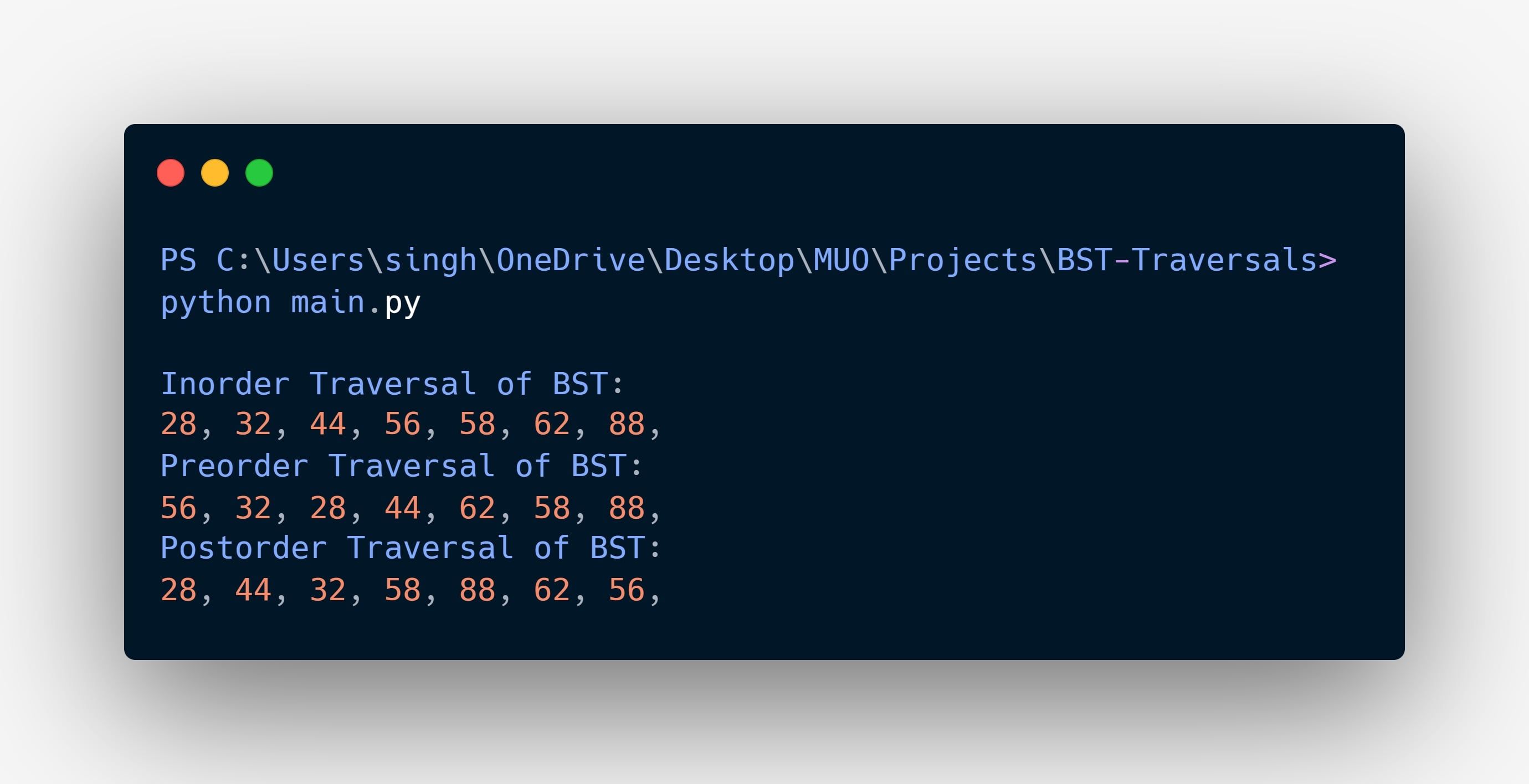
این برنامه باید خروجی زیر را تولید کند:
الگوریتم های ضروری برای برنامه نویسان
الگوریتم ها بخش مهمی از سفر هر برنامه نویسی هستند. برای یک برنامه نویس بسیار مهم است که به الگوریتم ها مسلط باشد. شما باید با برخی از الگوریتمهایی مانند مرتبسازی ادغامی، مرتبسازی سریع، جستجوی باینری، جستجوی خطی، جستجوی اول عمق و غیره آشنا باشید.
