نمودار یک ساختار داده همه کاره است، با انواع مختلف. شما می توانید از آن برای حل بسیاری از مشکلات استفاده کنید، به ویژه مشکلاتی که در کارهای مصاحبه مطرح می شوند.
یک برنامه نویس موثر نیاز به درک کاملی از ساختارهای داده و الگوریتم ها دارد. مصاحبه های فنی اغلب مهارت های حل مسئله و تفکر انتقادی شما را آزمایش می کند.
نمودارها یکی از بسیاری از ساختارهای داده مهم در برنامه نویسی هستند. در بیشتر موارد، درک نمودارها و حل مسائل مبتنی بر نمودار آسان نیست.
نمودار چیست و چه چیزهایی باید در مورد آن بدانید؟
نمودار چیست؟
گراف یک ساختار داده غیر خطی است که دارای گره ها (یا رئوس) با یال هایی است که آنها را به هم متصل می کند. همه درختها زیرگرافها هستند، اما همه نمودارها درخت نیستند، و نمودار ساختار دادهای است که درختها از آن سرچشمه میگیرند.
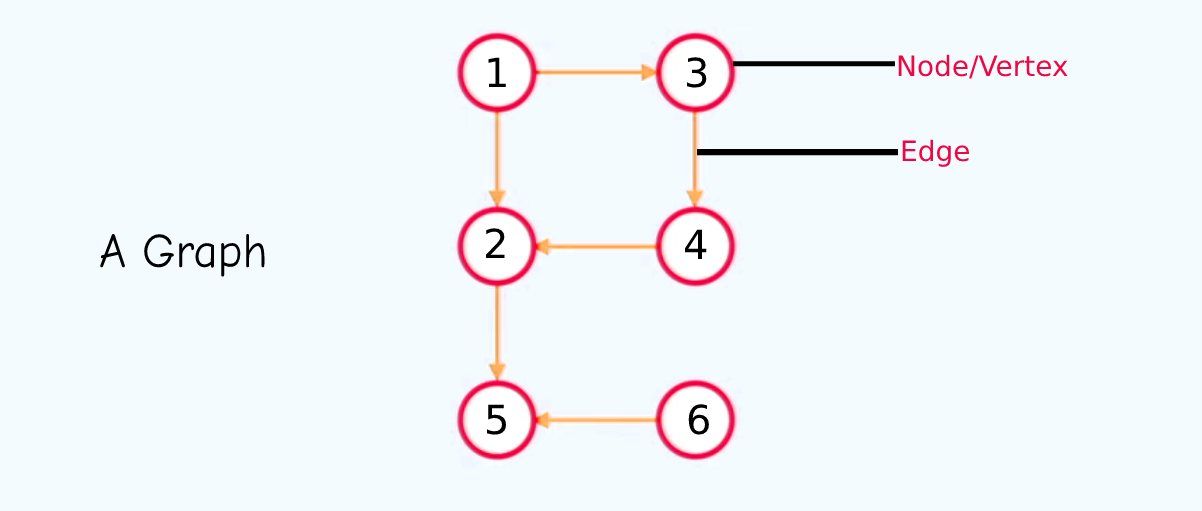
اگرچه میتوانید ساختارهای داده را در جاوا اسکریپت و زبانهای دیگر بسازید، اما میتوانید یک نمودار را به روشهای مختلف پیادهسازی کنید. محبوب ترین رویکردها لیست لبه، لیست مجاورت و ماتریس مجاورت هستند.
راهنمای نمایش نمودارها آکادمی خان منبعی عالی برای یادگیری نحوه نمایش نمودار است.
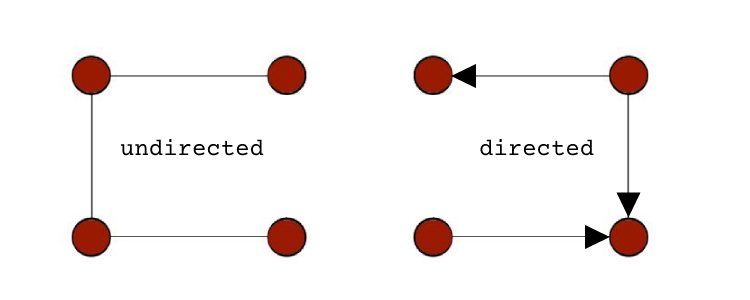
انواع مختلفی از نمودارها وجود دارد. یک تمایز مشترک بین گراف های جهت دار و غیر جهت دار است. این موارد در چالشهای کدنویسی و استفادههای واقعی بسیار مطرح میشوند.
انواع نمودارها
- گراف جهت دار: نموداری که در آن تمام یال ها دارای جهت هستند که به آن دیگراف نیز گفته می شود.
- گراف بدون جهت: گراف بدون جهت به عنوان گراف دو طرفه نیز شناخته می شود. در نمودارهای بدون جهت، جهت یال ها اهمیتی ندارد و پیمایش می تواند به هر جهتی انجام شود.
- نمودار وزنی: گراف وزن دار، گرافی است که گره ها و لبه های آن دارای یک مقدار مرتبط هستند. در بیشتر موارد، این مقدار نشان دهنده هزینه کاوش در آن گره یا لبه است.
- گراف محدود: گرافی که دارای تعداد محدودی گره و یال است.
- گراف بی نهایت: گرافی که دارای تعداد بی نهایت گره و یال است.
- گراف بی اهمیت: گرافی که فقط یک گره و بدون لبه دارد.
- نمودار ساده: زمانی که تنها یک یال هر جفت گره گراف را به هم متصل کند، آن را گراف ساده می نامند.
- گراف پوچ: گراف پوچ گرافی است که هیچ لبه ای برای اتصال گره های خود ندارد.
- مولتی گراف: در یک مولتی گراف، حداقل یک جفت گره بیش از یک یال دارند که آنها را به هم متصل می کند. در مولتی گراف ها، حلقه های خود وجود ندارد.
- گراف کامل: گراف کامل گرافی است که در آن هر گره به هر گره دیگری در گراف متصل می شود. به عنوان نمودار کامل نیز شناخته می شود.
- شبه گراف: گرافی که دارای حلقه خود به غیر از لبه های دیگر گراف باشد، شبه گراف نامیده می شود.
- گراف منظم: گراف معمولی گرافی است که در آن همه گره ها دارای درجات مساوی هستند. یعنی هر گره به همان تعداد همسایه دارد.
- گراف متصل: گراف متصل به سادگی هر گرافی است که در آن هر دو گره به هم متصل شوند. یعنی یک گراف با حداقل یک مسیر بین هر دو گره گراف.
- گراف قطع شده: گراف قطع شده برعکس گراف متصل است. در یک گراف قطع شده، هیچ لبهای وجود ندارد که گرههای گراف را به هم پیوند دهد، مانند گراف پوچ.
- گراف چرخهای: گراف چرخهای، گرافی است حاوی حداقل یک چرخه نمودار (مسیری که به همان جایی که شروع شده به پایان میرسد).
- گراف غیر چرخه ای: گراف غیر چرخه ای گرافی است که اصلاً چرخه ای ندارد. می تواند کارگردانی یا بدون کارگردانی باشد.
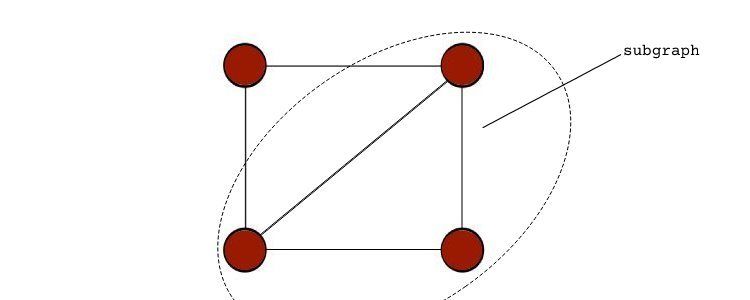
- زیرگراف: زیرگراف یک گراف مشتق شده است. این نموداری است که از گره ها و لبه هایی که زیرمجموعه های گراف دیگری هستند تشکیل شده است.
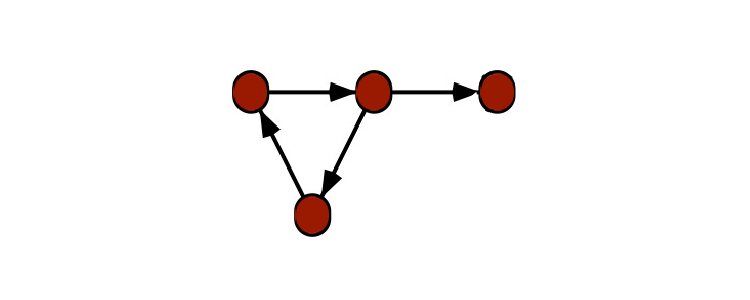
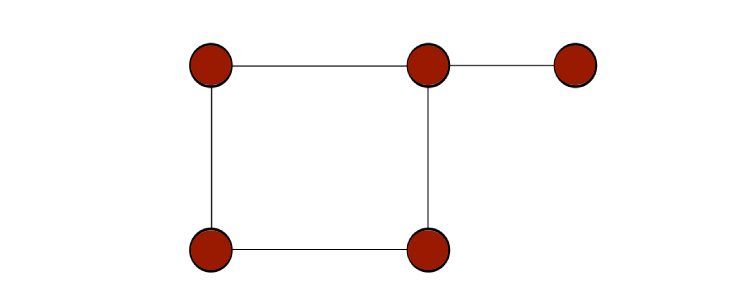
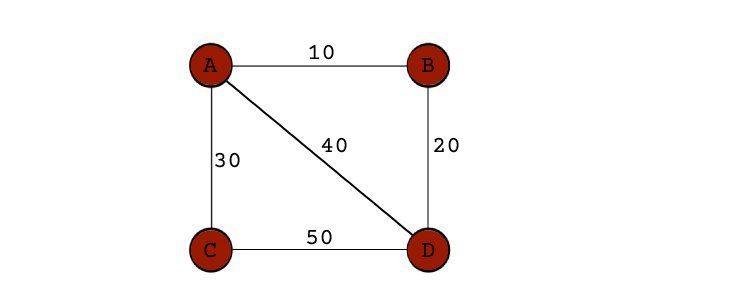
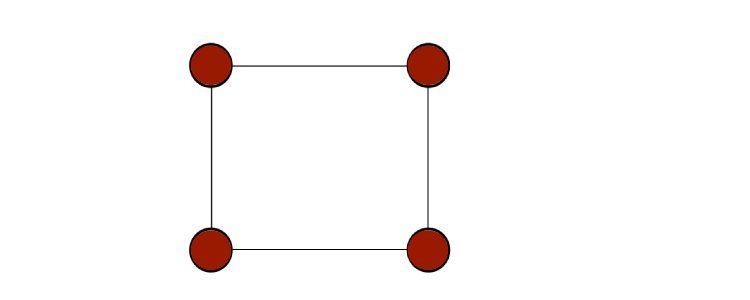
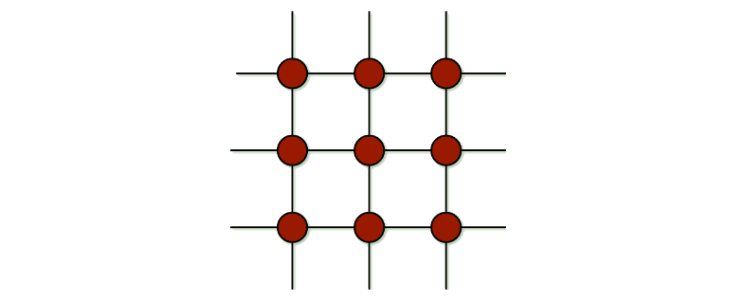

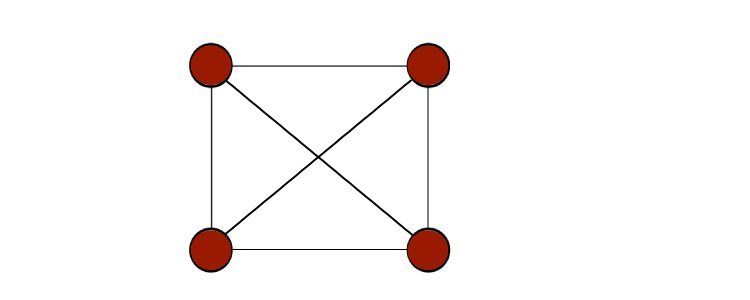
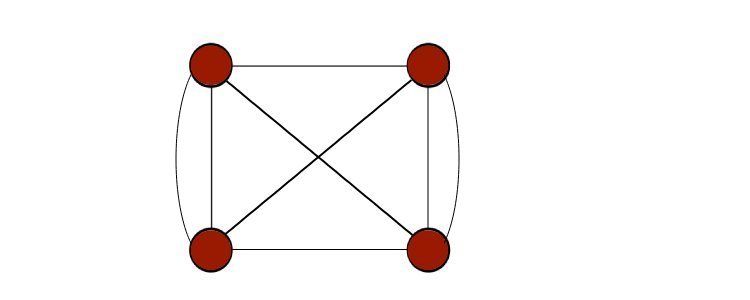
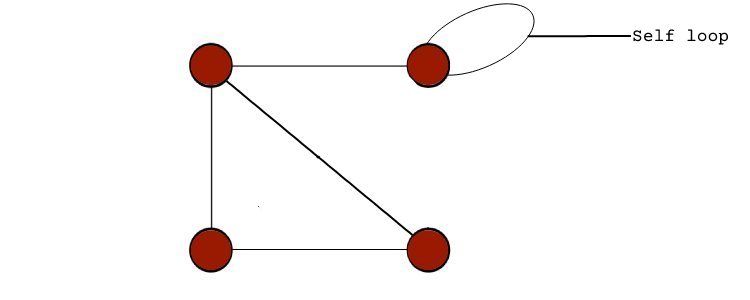
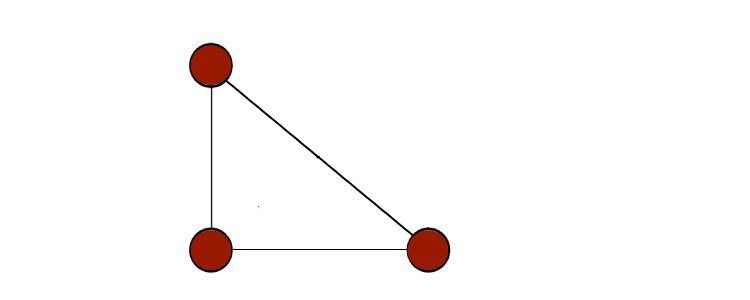
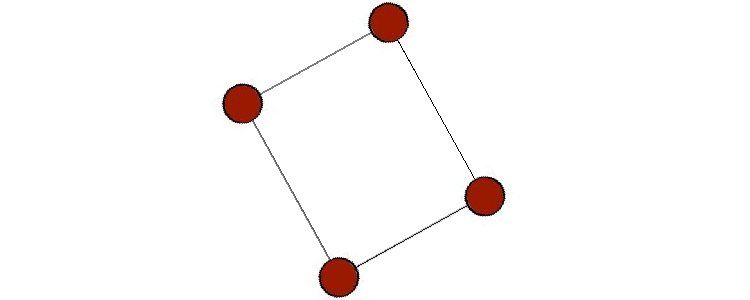
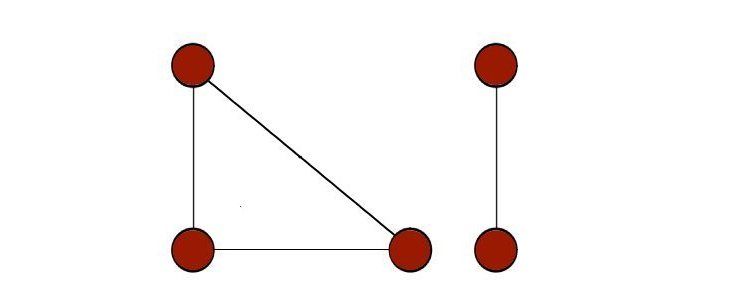
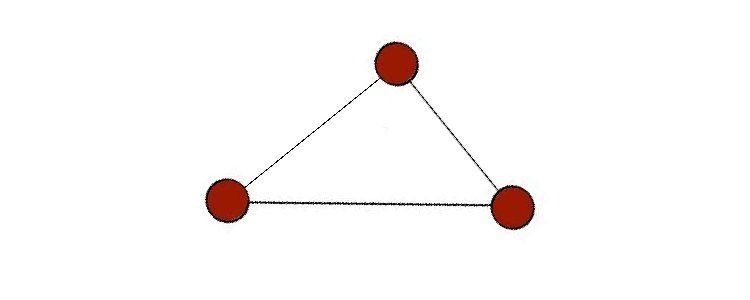
حلقه در گراف یالی است که از یک گره شروع شده و به همان گره ختم می شود. بنابراین، حلقه خود حلقه ای است بر روی یک گره گراف، همانطور که در شبه گراف دیده می شود.
الگوریتم های پیمایش نمودار
به عنوان یک نوع ساختار داده غیر خطی، عبور از یک نمودار بسیار مشکل است. عبور از یک نمودار به معنای عبور و کاوش در هر گره ای است که یک مسیر معتبر از طریق لبه ها وجود دارد. الگوریتمهای پیمایش نمودار عمدتاً دو نوع هستند.
- جستجوی اول عرض (BFS): جستجوی اول یک الگوریتم پیمایش گراف است که از یک گره گراف بازدید می کند و همسایه های آن را قبل از رفتن به هر یک از گره های فرزندش کاوش می کند. گرچه میتوانید از هر گره انتخابی یک نمودار را شروع کنید، گره ریشه معمولاً نقطه شروع ترجیحی است.
- Depth-First Search (DFS): این دومین الگوریتم اصلی پیمایش گراف است. این گره از گره گراف بازدید می کند و گره ها یا شاخه های فرزند خود را قبل از رفتن به گره بعدی کاوش می کند – یعنی ابتدا قبل از عریض رفتن به عمق می رود.
جستجوی Breadth-first الگوریتم پیشنهادی برای یافتن مسیرهای بین دو گره در سریع ترین زمان ممکن، به خصوص کوتاه ترین مسیر است.
جستجوی اول عمق بیشتر زمانی توصیه می شود که می خواهید از هر گره در نمودار بازدید کنید. هر دو الگوریتم پیمایش در هر صورت به خوبی کار می کنند، اما ممکن است یکی در سناریوهای انتخاب شده ساده تر و بهینه تر از دیگری باشد.
یک تصویر ساده می تواند به درک بهتر هر دو الگوریتم کمک کند. حالات یک کشور را به عنوان یک نمودار در نظر بگیرید و سعی کنید بررسی کنید که آیا دو حالت X و Y به هم متصل هستند یا خیر. یک جستجوی عمقی ممکن است در مسیری تقریباً در سراسر کشور انجام شود بدون اینکه به اندازه کافی متوجه شوید که Y فقط 2 حالت با X فاصله دارد.
مزیت جستجوی وسعت اول این است که قبل از رفتن به گره بعدی، تا حد امکان نزدیک به گره فعلی است. ارتباط بین X و Y را در مدت کوتاهی بدون نیاز به کاوش در کل کشور پیدا می کند.
تفاوت عمده دیگر این دو الگوریتم در نحوه پیاده سازی آنها در کد است. جستجوی عرضی یک الگوریتم تکراری است و از یک صف استفاده میکند، در حالی که جستجوی اول عمق معمولاً به عنوان یک الگوریتم بازگشتی اجرا میشود که پشته را تحت تأثیر قرار میدهد.
در زیر تعدادی شبه کد وجود دارد که اجرای هر دو الگوریتم را نشان می دهد.
جستجوی عرض-اول
bfs(Graph G, GraphNode root) {
let q be new Queue
// mark root as visited
root.visited = true
// add root to the queue
q.enqueue(root)
while (q is not empty) {
let current be q.dequeue() // remove front element in the queue
for(neighbors n of current in G) {
if (n is not yet visited) {
// add to the queue - so you can explore its neighbors too
q.enqueue(n)
n.visited = true
}
}
}
}
جستجوی عمق-اول
dfs(Graph G, GraphNode root) {
// base case
if (root is null) return
// mark root as visited
root.visited = true
for (neighbors n of root in G)
if (n is not yet visited)
dfs(G, n) // recursive call
}
تعدادی دیگر از الگوریتمهای پیمایش گراف از جستجوهای عرضی و عمقی اول استخراج میشوند. محبوب ترین آنها عبارتند از:
- جستجوی دوطرفه: این الگوریتم روشی بهینه برای یافتن کوتاه ترین مسیر بین دو گره است. از دو جستجوی گسترده استفاده می کند که اگر مسیری وجود داشته باشد با هم برخورد می کنند.
- مرتب سازی توپولوژیکی: در نمودارهای جهت دار برای مرتب سازی گره ها به ترتیب دلخواه استفاده می شود. شما نمی توانید یک مرتب سازی توپولوژیکی را برای نمودارهای بدون جهت یا نمودارهای دارای چرخه اعمال کنید.
- الگوریتم Dijkstra: این نیز نوعی BFS است. همچنین برای یافتن کوتاه ترین مسیر بین دو گره در یک گراف جهت دار وزن دار، که ممکن است دارای چرخه باشد یا نداشته باشد، استفاده می شود.
سوالات متداول مصاحبه بر اساس نمودارها
نمودارها از جمله ساختارهای داده مهمی هستند که هر برنامه نویسی باید بداند. اغلب در مصاحبه های فنی سوالاتی در مورد این موضوع مطرح می شود و ممکن است با مشکلات کلاسیک مرتبط با موضوع مواجه شوید. اینها شامل مواردی مانند مشکلات «قاضی شهر»، «تعداد جزایر» و «فروشنده دوره گرد» است.
اینها تنها تعدادی از مشکلات مصاحبه مبتنی بر نمودار محبوب هستند. می توانید آنها را در LeetCode، HackerRank یا GeeksforGeeks امتحان کنید.
آشنایی با ساختارها و الگوریتم های داده های نمودار
نمودارها فقط برای مصاحبه های فنی مفید نیستند. آنها دارای موارد استفاده در دنیای واقعی نیز هستند، مانند شبکهسازی، نقشهها و سیستمهای خطوط هوایی برای یافتن مسیرها. آنها همچنین در منطق اساسی سیستم های کامپیوتری استفاده می شوند.
نمودارها برای سازماندهی داده ها و کمک به ما در تجسم مسائل پیچیده بسیار عالی هستند. اگرچه برای جلوگیری از پیچیدگی فضا یا مشکلات حافظه، از نمودارها فقط باید در مواقع ضروری استفاده شود.